이 글 시리즈는 zzsza.github.io/data/2018/02/17/datascience-interivew-questions/에 있는
<데이터사이언스 인터뷰 질문 모음집>에 스스로 대답해보면서 정리해보고자 적어가는 글입니다.
주인장 분께 감사의 말씀 드립니다!
리샘플링의 다양한 방법론들, 1편
- 이번 글에서는 먼저 리샘플링의 첫번째 정의였던 부분부터 시작해보자(지난 글 참고)
- 그러나 본질적으로는 지난 글에서 구체화했듯이 두 정의가 크게 다르지 않다.
1. Estimating the precision of sample statistics by using subsets of available data(jackknifing) or drawing randomly with replacement from a set of data points (bootstrapping)
(1) 잭나이핑(Jackknifing)
- 먼저 잭나이핑부터 시작해 보자.
- 잭나이핑은 LOOCV(Leave-one-out Cross Validation)을 알고 있는 사람이라면 굉장히 친숙할 수 있는 개념이다.
- 근데 한편으로 LOOCV랑 헷갈리기도 쉽다.
- 잭나이핑은 쉽게 설명하자면 다음과 같다.
1) 전체 데이터에 대해 원하는 통계량(예)평균)을 구해본다. 이는 이전 글에서 이야기했듯 내가 가지고 있는 샘플에 편향된 통계량일 가능성이 있다.
2) 이번에는 전체 데이터에서 딱 하나의 샘플만 빼놓고(이 부분에서 LOOCV랑 비슷) 나머지 데이터의 평균을 구해본다.
3) 2)를 모든 샘플에 대해서 진행한다.
4) 3)은 결과적으로 sample mean의 distribution을 형성할 것이다. 즉, 샘플의 평균이 전체적으로 어떠한 분포를 그리고 있는지 확인이 가능하다.
5) 또한, 3)의 모든 결과를 평균을 내면, 실제로 1)과 동일한 값이 나오는 것이 수학적으로 증명이 되어 있다.

- 물론 평균 뿐만 아니라 더 높은 차수의 적률(분산 등)에서도 동일하게 분포를 구해볼 수 있다.
- 잭나이핑은 전체 샘플을 사용해 계산한 추정량(estimator)가 얼마나 편향되어 있는지(biased)를 측정해보는 도구로도 사용 가능하다.
- 예를 들어 H^가 우리가 진짜 알기를 원하는 어떤 모집단의 모수 H*에 대해서 구한 추정량이라고 하자(지난 글의 논리적 흐름과 같다). 이 때 잭나이핑으로 구한 추정량 H''을 평균을 내어 다음과 같은 값을 얻었다.

- 이 때, 잭나이프 추정량의 편향도는 다음과 같이 구할 수 있다.

- 이 값을 이용해 편향이 제거된(bias-corrected) 추정량을 다음과 같이 얻을 수 있다. 쉽게 말하면 추정량에서 잭나이핑을 이용해 계산한 편향값을 뺀 것.

- 잭나이프 연산값을 이용해 잭나이프 표준오차(SE, 잘 모른다면 공돌이의 수학노트님의 깃허브에 잘 정리되어 있다)를 구할 수도 있다.

- 잭나이핑의 장점으로는 연산이 심플하다는 것.
- 그러나 non-smooth statistics(중위수), non-linear stat(상관계수)등에 대해서는 성능이 잘 안 나온다고 한다(이유는 정확히 모름... 관련 논문이 있을지.. 혹시 아시는 분 있으면 댓글 부탁드립니다. 출처는 www.datasciencecentral.com/profiles/blogs/resampling-methods-comparison)
- 또한 샘플간의 iid(independent and identically distributed) 가정을 하고 있기 때문에, 시계열 데이터에서는 직접적인 사용이 힘들 수 있다.
- 또한 딱 한 관측치/행/샘플만 빼놓고 진행하기 때문에, 각 잭나이프 시행값간의 변동량이 그리 크지는 않을 것이다(샘플이 1000개가 있는데 a라는 샘플 빼놓고 999개 가지고 평균을 구한다고 b라는 샘플 빼놓고 나머지 999개 가지고 평균을 구하는 것과 그리 크게 다를까?)
(2) 부트스트래핑 (Boostrapping)
- 부트스트래핑은 머신러닝을 배웠다면 '교차검증' 파트에서 한 번쯤은 들어보았을 단어다.
- 물론 여기서 다루는 부트스트래핑과 사실상 동일 개념이다.
- 위키피디아에 따르면 부트스트래핑은
'Any test or metric that uses random sampling with replacement'
로 정의된다. - 부트스트래핑은 샘플 통계량(추정치)의 정확도(accuracy)를 측정하는 방법이다(지금까지 논의했듯이)
- (또 지금까지 논의했듯이) 모집단의 모수에 대한 단일 추정량에 대해 확실하지 않을 때 이에 대한 statistical infernce를 시행하는 방법이다.
- 쉽게 말하자면, 내가 가지고 있는 샘플에서 임의의 랜덤 샘플을 다시 추출(resampling)하되, 한 번 추출되었던 샘플 또한 다시 포함될 수 있도록 하는 복원추출법(sampling with replacement)을 적용한다.
예) 모집단 : (a,b,c,d,e)
복원추출샘플 예 : (a,a,b,b,e) - a,b 등이 '복원'되어 추출됨
- 다시 한 번 우리가 뭘 하고 있는지 짚고 넘어가기 위해, 모집단의 분포 J가 있다고 하자.
- 우리는 이 모집단의 분포 J에 대해 관심이 있지만, 실제로 정확히 J를 측정할 수는 없고, 대신 우리가 얻은 표본의 분포 J^이 있다.
- J^에 대한 추론은 어느정도 J에 대한 힌트를 제공하지만, 정확하지는 않다 (지난 글에서 S~P 문제라고 정의했던 부분을 기억해보자)
- 부트스트래핑을 이용해 J^에 대한 추론을 진행하고, J^에 대한 추론이 J, 즉 모집단의 찐분포에 유사(analogous)할 것이라고 가정하는 것이다.
- (다음은 위키피디아에 제시되어 있는 예시다)
예를 들어 전 세계 사람들의 키 분포를 알고 싶다고 해 보자. - 전 지구 사람들의 키를 다 재 볼수는 없지 않겠는가?
- 그래서 N명의 샘플(S1라고 하자)을 뽑아 그들의 키를 재 보고, 그 평균을 내 보고, 이를 S1_A라고 하자.
- 이 평균 S1_A는 전 세계 사람들의 키 분포에 대해 믿을만한 정보를 제공한다고 할 수 있을까?
- S2_A, S3_A, ... 즉, 샘플을 다르게 뽑으면 평균 또한 달라질 것이다.
- 이 평균 값들을 모아놓은 벡터 혹은 집합을 S_A라고 하자.
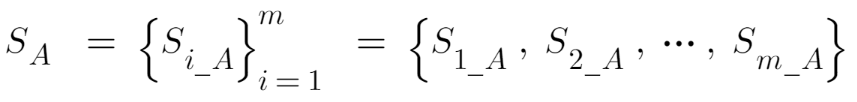
- 이 벡터의 히스토그램을 R, 파이썬 등을 통해서 그려보았다고 하자.
- 그러면 이는 전 세계 사람들의 키의 샘플 평균의 분포에 대한 좋은 추론이 될 것이다.
- 그런데 문제는 샘플을 다르게 뽑기가 힘들다는 것이다. 모집단에서 매번 샘플을 뽑는게 물리적/비용적으로 불가능할 수 있다.
- 그래서 주어진 샘플 S1에서 S1a, S1b, ... 등으로 복원추출을 시행하고, 이를 통해 부트스트랩 평균값 벡터를 뽑아내어, S_A를 대체하는 것이다.
- 부트스트랩의 장점이 무엇이 있을까?
- 먼저 굉장히 직관적이고 직접적(starightforward)이다.
- 예를 들어 구한 추정치의 신뢰구간(confidence interval of the sample estimate)을 알고 싶다고 하면, 기초적으로 통계학에서 배우는 신뢰구간 추정법, 즉 샘플 분산과 normality 가정을 이용해 구하는 것보다 더 정확하게 모집단의 true confidence interval에 대한 추론을 제시할 것이다.
- 그렇다면 부트스트랩의 단점은 무엇일까?
- 어떻게 보면 당연한 얘기지만, 내가 지금 뽑아둔 샘플 S1의 샘플 퀄리티가 구리다면 (한쪽으로 치우치고 편향된 샘플 추출 등), 즉 S1이 P에 대한 충분히 괜찮은 모형이 아니라면, 부트스트랩은 철저히 S1에 의존하기 때문에 부트스트랩 결과물 또한 구릴 수 밖에 없을 것이다.
- 그래서 최대한 부트스트랩 샘플 추출을 여러 번 하는 것이 중요하다. 최대한 원 샘플에 대한 의존성이 줄어들도록.
- 또한 샘플 안의 관측치의 양 (number of samples)이 너무 많다고 해서 크게 좋을 건 없다고 한다. 부트스트랩 논문 원 저자는 논문에서 샘플양을 50개로 했다고...
- 이 외에 부트스트래핑을 실현하기 위한 다양한 방법론으로 Case resampling, Bayesian bootstrapping, Smooth bootstrap, Parametric bootstrap(모집단에 대한 가정을 하고 진행하는) 등이 있다. 이를 여기서 다 다루기는 힘들 듯...
다음 글에서는 교차검증(cross validation)에 대해 다뤄보도록 하겠습니다.
더 궁금하신 부분들이 있으면 아래 출처를 살펴보시면 좋을 것 같습니다.
출처)
잭나이핑 위키 en.wikipedia.org/wiki/Jackknife_resampling
부트스트래핑 위키 en.wikipedia.org/wiki/Bootstrapping_(statistics)
Boston University 학습자료 people.bu.edu/aimcinto/jackknife.pdf
'이은혜 수학 공간' 님의 블로그, <부트스트랩 샘플링이란?> m.blog.naver.com/PostView.nhn?blogId=mathnstat&logNo=221404758083&proxyReferer=https:%2F%2Fwww.google.com%2F
Harvard University, Stat 221 학습자료 sites.fas.harvard.edu/~stat221/spring-2006/intro/bootstrap.pdf
<Bootstrapping vs. jackknife>, Ly Nguyenova, Medium
medium.com/@lymielynn/bootstrapping-vs-jackknife-d5172965207b
<A Gentle Introduction to Statistical Sampling and Resampling>, Jason Brownlee
machinelearningmastery.com/statistical-sampling-and-resampling/
'수학 및 통계학 > 수리통계학' 카테고리의 다른 글
| 확률분포의 모수 추정, (1) 표본분포와 중심극한정리 (0) | 2021.03.30 |
|---|---|
| (베이지안) 가우시안(Normal) 분포와 베이지안 접근법의 기초 (0) | 2021.03.20 |
| (데이터과학 인터뷰 질문) (7) 확률분포 1. 베르누이와 이항분포 (0) | 2021.03.03 |
| (데이터과학 인터뷰 질문) (6) 확률변수와 확률모형의 차이 (0) | 2020.11.10 |
| (데이터과학 인터뷰 질문)(2) 샘플링과 리샘플링, 1편 (0) | 2020.10.28 |



