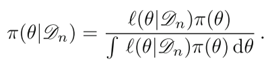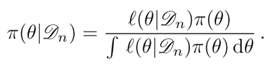이 글은 개인적으로 공부한 내용을 간략하게 정리하기 위한 포스팅입니다. 상세한 내용은 전공 교재들을 참고하시는 것이 좋습니다.
Normal Modeling
-
가우시안 분포는 다음과 같은 수식의 PDF를 갖는 함수다.
-
수많은 분야에서 적용되는 분포다. 이는 이 분포가 가지고 있는 ‘정상성’(normality) 때문.
-
작은 사건들이 모여 극한에서는 normal한 모습을 보이는 실제 데이터들
-
긴 꼬리(long tail)를 갖지 않는 대칭분포 현상들을 아주 잘 적합하는 모델.
-
수식의 수학적 특성 때문에(해석학적 특성 및 닫힌 꼴의 연산).
-
따라서 많은 모델링 수업의 첫 발걸음.
-
심지어 심플한 포아송이나 이항분포보다도 더욱 introductory.
-
그렇다고 해서 가우시안 분포가 모든 현상을 다 설명하는 킹왕짱 분포는 아니다.
-
다양한 이유로 인해(예. 왜도, 분포의 두꺼운 꼬리 현상, 독립성 충족 X, n봉분포 등) 가우시안이 잘 안 먹혀드는 경우가 존재.
-
노멀 분포는 어쨌든 피팅만 어느정도 해 주면 잘 설명해주는 경우가 많다.
-
즉, ‘true distribution’에 근접할 가능성이 높다(그런게 존재한다면 말이다)
-
아주 가끔은 (상황이 잘 맞아떨어지면) true distribution이 정말로 노멀이라고 말할 수 있는 경우가 있다.
Bayesian Toolkit
사후확률분포(Posterior)
-
개념을 잡기 위해 i.i.d 가정이 되어 있는 normal 분포에서 얻은 샘플을 생각해보자.
-
이 때 가능도 함수(likelihood function)을 다음과 같이 정의한다.
-
-
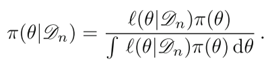
RHS: 미지의 모수 theta가 주어졌을 때, 모든 data point들 x_i에 대한 함수의 곱
-
LHS: 데이터가 주어졌을 때 모수 theta에 대한 함수
-
샘플 D_n은 theta에 대한 정보를 주고, 이를 이용하여 theta에 대한 추론을 이끌어낸다.
-
예를 들어, D_n이 가우시안 분포로부터 온 샘플이고, size = n이라면 가능도 함수는 다음과 같다.
-
Proportional한 이유는 theta가 아닌 D_n에 관련된 값들을 쳐 냈기 때문이다.
-
물론 이러한 접근법은 parameter가 많아질 때 굉장히 위험할 수 있다.
-
베이즈 통계학의 가장 큰 차별점은 이렇게 얻어낸 정보를 posterior에 반영시킬 수 있다는 것이다. 이는 베이즈 정리를 이용한다.
-
Π(θ)는 prior다.
-
이는 θ에 대한 ‘확률분포’다. 근데 그렇다고 해서 θ가 꼭 진짜 ‘확률변수’ 일 필요는 없다. 왜냐하면 inferential tool로 쓰기 위해서 구하는 것이지, 진짜 확률분포로서 사용하려고 하는 게 아니기 때문이다.
-
Prior 분포는 왜 필요할까? Prior 분포는 θ에 대한 prior information을 요약한다.
-
다시 말하면 데이터를 관측하기 전 가지고 있는 모수 θ에 대해 갖고 있는 지식이다.
-
그런데 이 사전분포는 소위 ‘도메인 지식’에 의존하는 경우가 많다.
-
이러한 베이지안 방식의 접근법은 모수 θ에 대한 inference에 대한 확률적 프레임워크(probabilistic framework)를 제공한다.
-
예를 들어, 분산이 알려져 있는 가우시안 분포 N(μ,σ^2)를 생각해 보자.
-
만약 μ에 대한 prior가 동일한 분산을 갖고 평균이 0인 N(0,σ^2) 가우시안 분포라고 하자.
-
이 때, posterior는 베이즈 정리를 이용하여 다음과 같이 구할 수 있다.
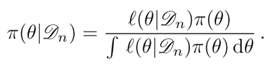베이즈 정리(Bayes Theorem)
Bayes Theorem을 이용해 구한 posterior
-
이 수식과 Gaussian PDF를 잘 비교해보면 (x로 표시되어 있는 걸 μ로 바꾸면 된다. 지금 μ에 대한 분포니까) 평균이 n x̅/(n+1) , 분산이 σ^2/(n + 1)인 Gaussian PDF임을 알 수 있다.
-
분포가 달라졌으므로 posterior의 n차 적률값도 달라질 것이다.
-
어떻게 달라지냐면, 기존 Gaussian보다 조금 더 0 근방의 밀집도가 높아질 것이다.
-
왜냐하면, Bayes Theorem을 통해 prior의 정보, 곧 μ가 평균이 0이고 분산이 σ^2이라는 정보가 Posterior에 반영되었기 때문이다.
-
만약 μ ~ N(10, σ^2)이었다면, 10쪽으로 조금 더 모였을 것.
