(PRA) 회귀분석 1. 데이터 분석의 전반적 컨셉

이 시리즈는 Practical Regression and Anova using R, JJ Faraway, 2002를 공부하면서 정리했습니다. 개인적 사용을 위한 copyright 제한을 따로 걸어두지 않았고 pdf도 무료배포 중입니다. 회귀분석 운을 떼기에 좋은 책이라고 생각합니다. 수학적으로 엄밀하게 증명하면서 따져가는 책은 아니고 multivariate case는 살펴보지 않게 됩니다. 

 

 

 

 

---

* 데이터 분석에 대한 전반적 소고

 

• 통계학은 '문제의식'으로부터 시작됩니다.
• 따라서 문제가 무엇인지 정확히 인지하는 것이 중요합니다.

 

• 이를 위해 다음과 같은 사항을 생각해봅시다.
  • 흔히 도메인 지식이라고 부르는, 주어진 데이터의 underlying background를 항상 고려합시다.
  • 분석의 목적이 무엇인지 명확히 인식합시다.
  • 분석 고객의 의중과 요구사항이 무엇인지 정확히 인지합시다.
  • 분석 문제를 통계학적 용어로 번역합시다.
• 데이터가 어떻게 수집되었는지 이해하는 것도 중요하고 필수적입니다.
  • 주어진 데이터는 실제로 수집된 데이터입니까, 아니면 시뮬레이션 된 데이터입니까?
  • 수집되지 않은 데이터는 왜 수집되지 않았을까요? 때로는 수집되지 않은 데이터가 수집된 데이터보다 더 중요할 수 있습니다.
  • 결측값이 존재합니까? 왜 결측값이 존재할까요?
  • 데이터가 어떻게 코딩되었습니가? 특히, 질적변수들이 어떻게 입력되었나요?
  • 측정 단위는 변수별로 어떻게 되어 있습니까?
  • 데이터가 입력될 때 오류가 발생하지는 않았습니까?(이것은 사실 실무에서는 너무나도 흔히 벌어지는 일)

 

• 처음 데이터를 분석하게 된다면 흔히들 말하는 EDA라는 과정을 겪게 될 것입니다. EDA는 단순해 보이지만 데이터의 이해와 모델링에 필수적입니다.
  • 수치적 요약 - n차 적률(평균, 분산, 왜도, 첨도, 상관관계 등...)
  • 시각적 요약
    • 일변량: 박스플랏, 히스토그램
    • 이변량: 산점도
    • 다변량: 상호작용성 플롯
  • 이 과정에서 아웃라이어, 입력 오류, 왜도 및 비정상적인 분포를 찾아야 합니다. 데이터가 당신이 예상하던 대로 분포되어 있나요?
• 이 과정을 교재에서 제공하는 예제를 통해 살펴봅시다

• 총 9개의 변수를 가지고 있는 데이터프레임을 확인할 수 있습니다.
• 미국 피닉스 근방에 사는 Pima 인디언들의 Diabetes test 결과를 확인하고 측정한 데이터입니다.
• 데이터를 더 잘 이해하기 위해 변수명을 한국어로 잠시 바꿔봅시다.

 

• summary() 함수는 R의 강력한 요약통계 함수입니다. 각 변수의 요약통계치를 제시해줍니다.

 

• 이 값들을 하나하나 살펴보면서 이상한 점이 있는지 알아봅시다. 앞에서 말했듯이 혹시 분포가 이상하거나 혹은 데이터 입력이 잘못된 경우를 알아보아야 합니다.
• 최소,최대값은 이 문제에 대해 좋은 정보를 제공해주죠. min값들을 살펴봅시다. 임신횟수가 0회인건 전혀 이상한 게 아니지만, 혈당이나 혈압이 0이라는건 뭔가 상당한 문제가 있다는 뜻이겠죠? 혈압을 한 번 살펴봅시다.

• 35명의 혈압 값이 0으로 입력되어 있는 것을 알 수 있네요. 혈압이 실제로 0이었을리는 없으니 아마도 결측값을 0으로 처리한 것이 아닐까 하는 생각을 해 볼수 있습니다.
• 실무에서는 당연히 이런 경우 데이터를 입력한 인원에게 무슨 일이 일어났으며, 0값은 무엇을 의미하는지 커뮤니케이션을 통해 알아보아야 합니다. 만약 아무 생각없이 이 값들을 그대로 모델링에 활용하게 되면 굉장히 잘못된 결과를 불러일으킬 수 있겠죠?
• 혈장혈당:BMI까지의 0값들을 NA로 변환하도록 하겠습니다.

 

• 테스트 결과는 {0,1}의 값만을 갖는 질적 변수인데 numeric으로 입력되어있습니다. factor로 바꿉시다.

 

• 수치를 살펴보는 법을 아주 간단히 살펴보았습니다.
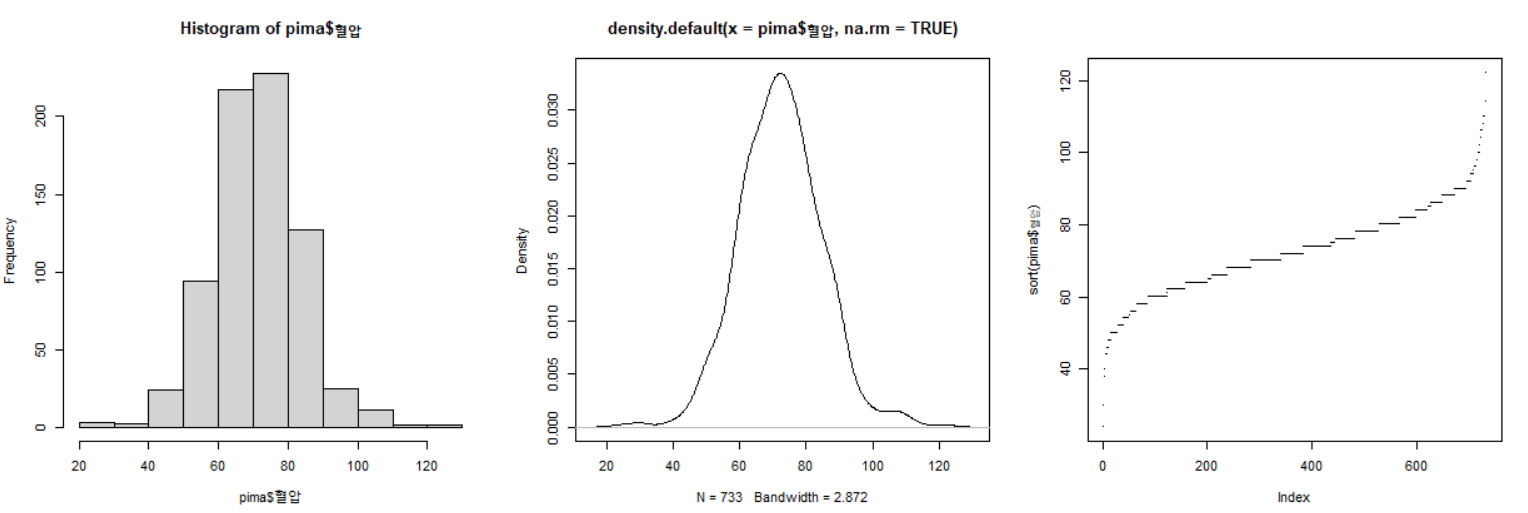
• 이제 일변량 시각화입니다. 다음의 세 플롯은 각각 히스토그램, 커널 밀도 플롯, 인덱스-데이터 플롯입니다. 인덱스 데이터 플롯은 해당 벡터를 오름차순으로 정렬하여 possible outlier를 찾는 데에 도움이 됩니다.
• 히스토그램과 밀도 플롯에서 bell-shape 분포를 확인할 수 있습니다.

 

 

• 다음은 이변량 시각화입니다. 여기서는 산점도와 박스플롯만 간단히 살펴보겠습니다.

혈압에 따른 혈장혈당 분포와 테스트 결과 별 혈장혈당 분포.

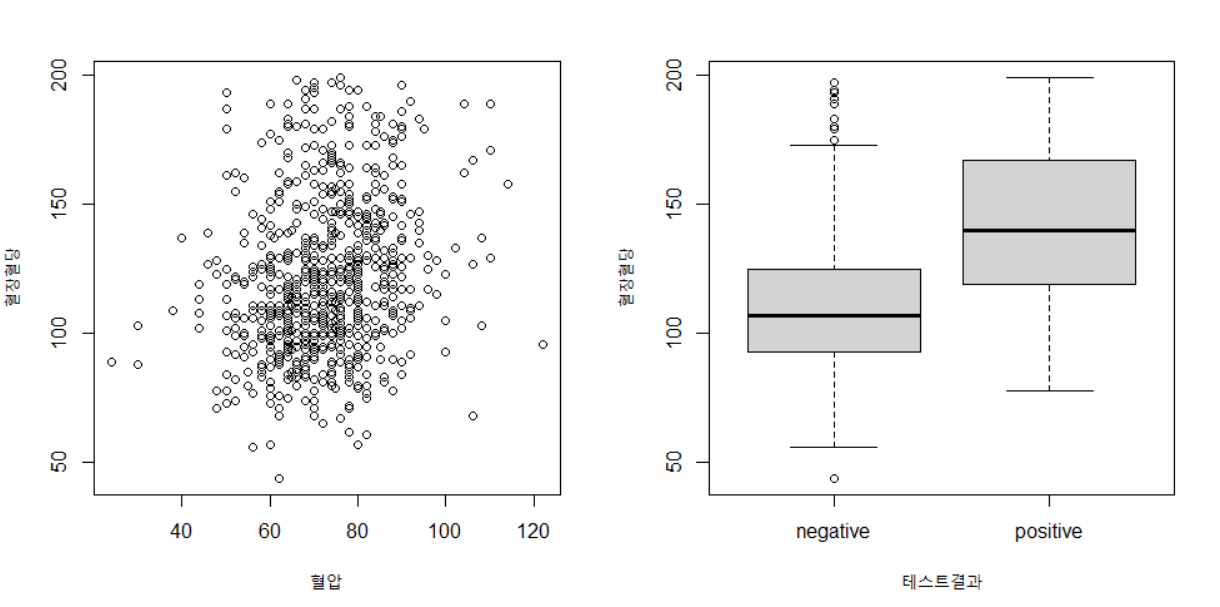
• 혈압과 혈당 사이에는 큰 상관관계가 없어 보입니다. 테스트 결과에 따른 혈당 분포는 확실한 차이가 있네요(평균에서). 책에서는 여기까지만 나와 있지만 저는 ggplot을 이용해서 첫 번째 산점도에 테스트결과를 색깔로 입혀 보겠습니다.

 

 

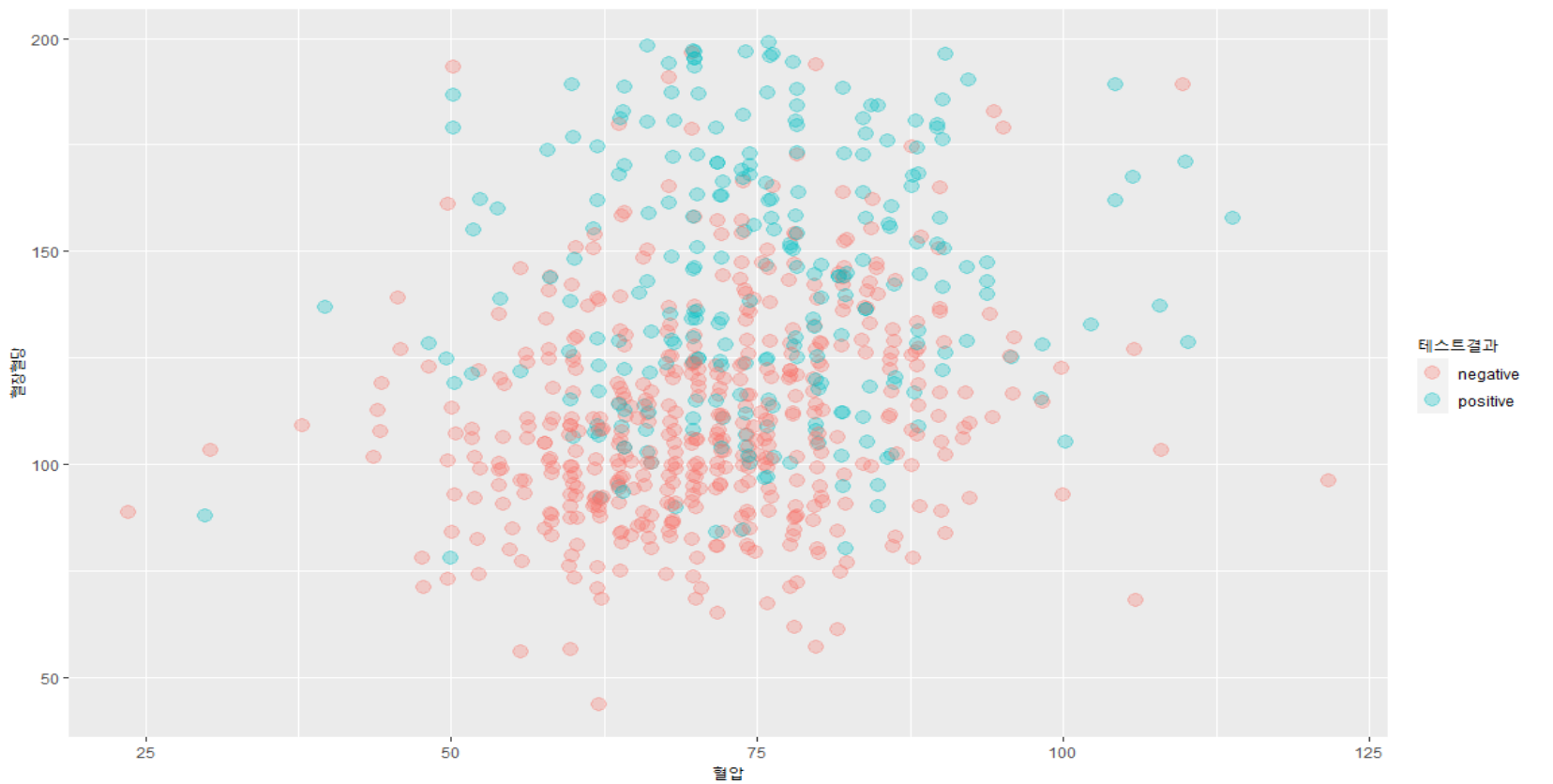
• 이 플롯을 보고 무엇을 알 수 있을까요? 사실 이 전에 얻었던 정보를 다시 확인하는 정도에 그치기는 합니다. 그러나 세 가지 변수를 이차원 플롯에서 확인할 수 있다는 건 분명한 메리트가 있죠.
  • 보시면 x축에서 값이 변화하는 것에 따라서는 테스트 결과가 크게 나뉘지는 않습니다.
  • 하지만 y축, 곧 혈당은 그 값이 변화함에 따라 test = positive한 경우가 훨씬 많아지는 것을 알 수 있습니다.
  • 어떻게 보면 당연한 결과죠. 직관적으로 P(당뇨 | 높은 혈당) > P(당뇨 | 낮은 혈당)일테니까요.
  • 위의 박스플롯에서도 확인한 결과입니다. 어쨌든 이렇게 산점도에서 약간의 조작을 통해 한 눈에 확인할 수 있다는 장점이 있습니다.
• pairs()함수를 이용하면 데이터 전체의 산점도를 한 번에 볼 수 있습니다. 물론 이 방법은 컬럼 수가 많아지면 사용이 힘듭니다.