(토막글 및 잡설) 선형회귀에서 '선형'의 의미

• 선형회귀는 처음 구축되었을 때나 지금이나 강력하고 유의미한, 이 세상을 설명하는 방법론입니다.
• 머신러닝과 딥러닝의 시대를 살아가고 있다고 이야기하는 지금도 선형회귀모형의 기본 아이디어, 즉
  
  (세상의 어떠한 현상 Y) = (적절한 변수들 X) + (X와 관계없는 잡음 u)
  
  로 모델링할 수 있다는 일종의 신념(?)은 사실상 머신러닝과 딥러닝에서도 동일하게 스며들어 있습니다.
• 다만 머신러닝과 딥러닝은 이를 갈수록 발전하는 computational capacity를 이용하여 해결하고자 하는 것이지요. 그 단적인 예가 요새 캐글에서 유행하는 GB(Gradient Boosting) 계열의 알고리즘들이지 않을까 생각합니다(GB가 error term u에 대해서 접근하는 방식을 생각해보세요)

 

• 어쨌든, 선형회귀가 복잡한 머신러닝?을 배우기 이전의 일종의 입문단계 방법론처럼 비추어지는 것이 아쉬운 점들이 많습니다. 그러한 맥락에서 여러 블로그나 강의에서 선형회귀를 가르치고 또 포스팅하는 것을 볼 수 있는데요.
• 그 중에 다음과 같은 문장을 볼 때가 많습니다.
  
  "선형회귀는 다음과 같은 수식을 이야기합니다. Y = B0 + B1X라는 모형을 만드는데, 이는 우리가 중학교 때 배우는 일차방정식과 동일한데, 그 그래프를 생각해보면 직선의 형태를 띄고 있죠. 이렇게 선형의 모양을 가지고 있다고 해서 이를 선형회귀라고 이야기합니다. 따라서, 예를 들어 Y = B0 + B1X + B2X^2 등의 모형을 만든다면 이는 이차식의 형태를 띄고 있으므로 비선형회귀라고 할 수 있습니다."

 

• 근데 사실 이는 완전히(까지는 아니고 95%) 틀린 이야기입니다. 왜냐하면 선형회귀에서 선형은 변수(혹은 모수)의 선형결합(linear combination)으로 Y를 표현할 수 있다는 의미거든요.
• 이는 회귀모형을 matrix notation으로 표현한 교재를 보기 시작하면 분명해집니다.
  
  

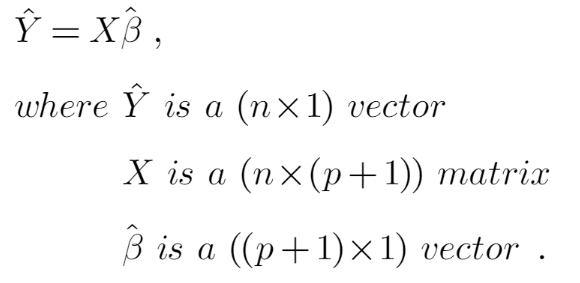
• 변수 X에 각 모수 B가 선형결합되어 Y를 계산하게 되는 것을 알 수 있죠.
• 선형이라는 이름은 여기서 나왔습니다. 최종 산출식의 그래프가 어떠한 형태를 띄고 있는지는 아무런 상관이 없습니다.
• 다음과 같은 식을 비선형 회귀 모형이라고 부릅니다. 즉, 변수의 선형결합으로 Y값을 나타낼 수 없는 경우죠.
  

• 그러나 실제 연구에서는 선형모형으로도 충분히 세상을 설명하는 것이 가능하다고 생각한다고 합니다.
• 즉, 중요한 것은 형태가 아니라 적절한 x의 선택이라는 거겠죠?

 

 

참고) Introductory Econometrics, a Modern Approach, Wooldridge, 7E